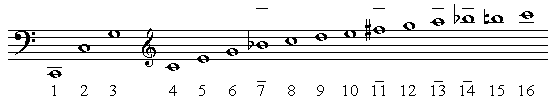Teiltöne in Cent
Die Teiltonreihe entspricht unserem Tonsystem nicht genau, sondern nur annähernd. Einige Töne sind erheblich tiefer als die entsprechenden Töne in der temperierten Stimmung. Bei ihnen steht im Notenbeispiel ein Strich über der Note und der Zahl.
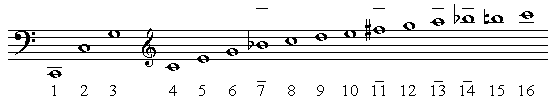
Man kann sich die genaue Größe der Abweichungen gut mit einer Tabelle klar machen.
Dazu wird die Teiltonreihe in Oktavabschnitte gegliedert.
Die fünf untersten Oktavabschnitte sind erfasst.
Die Tabelle zeigt die Höhe der Teiltöne über dem Grundton des
jeweiligen Oktavabschnitts der Teiltonreihe, und zwar in Cent.
Das Rechnen in Cent hat folgenden Vorteil:
Wenn man mit Schwingungszahlen oder
Saitenlängenverhältnissen rechnet, muss man multiplizieren und dividieren,
um die Verhältniszahlen von kombinierten Intervallen zu erhalten. Das ist
rechnerisch umständlich und nicht gut vorstellbar. Um die Größe von
Intervallen logarithmisch, besonders genau und unabhängig von unserem Tonsystem
angeben zu können, wird gewöhnlich in "Cent" gerechnet.
Anmerkung
Die Centrechnung unterteilt die Oktave in 1200 gleiche Schritte und
dementsprechend den temperierten Halbtonschritt in 100 Schritte.
Näheres zur Berechnung der Cent-Werte steht in der Extra-Datei
Berechnungsverfahren für die Cent-Werte
| 1. Oktave | 2. Oktave | 3. Oktave | 4. Oktave | 5. Oktave | |
| 1 | 2 | 4 | 8 | 16 | 0.000 |
| | | | 17 | 104.955 |
| | | 9 | 18 | 203.910 |
| | | | 19 | 297.513 |
| | 5 | 10 | 20 | 386.314 |
| | | | 21 | 470.781 |
| | | 11 | 22 | 551.318 |
| | | | 23 | 628.274 |
| 3 | 6 | 12 | 24 | 701.955 |
| | | | 25 | 772.627 |
| | | 13 | 26 | 840.528 |
| | | | 27 | 905.865 |
| | 7 | 14 | 28 | 968.826 |
| | | | 29 | 1029.577 |
| | | 15 | 30 | 1088.269 |
| | | | 31 | 1145.036 |
Anmerkung
Die Bezeichnung Cent wurde 1884 von A. J. Ellis eingeführt.
Das Rechnen mit Intervalllogarithmen beginnt vermutlich 1637 mit
Francesco Bonaventura Cavalleri, siehe
Martin Ebeling, Tonhöhe physikalisch - musikalisch - psychologisch - mathematisch,
Frankfurt 1999, S. 37ff. zurück
www.stefanprey.de
Hauptseite